From Text to Numbers: How Computers Convert Strings to Integers Under the Hood

An in-depth exploration of how computers transform textual representations of numbers into actual integers, with code examples in multiple languages and performance considerations.

Table of Contents

1. Introduction: The Hidden Magic Behind parseInt()

   • Overview of conversion functions

   • Importance of understanding internal mechanics

2. The Core Challenge: Computers Only Understand Numbers

   • Binary data processing

   • Numeric input as character codes

3. ASCII and Character Encoding: The Missing Link

   • ASCII representation of characters

   • Numeric character conversion using ASCII

4. Why We Can't Just Add ASCII Codes

   • Limitations of direct ASCII code summation

   • Distinction between ASCII codes and digit values

5. Multi-Digit Numbers: Position Matters

   • Positional number system

   • Decimal number representation

6. The Algorithm: Building Numbers Digit by Digit

   • General algorithm overview

   • Step-by-step example with "4327"

7. Implementing the Algorithm in C

   • Basic C implementation

   • Explanation of code mechanics

8. Seeing the Algorithm in Action: A JavaScript Implementation

   • JavaScript implementation

   • Testing with example input

9. Handling Edge Cases: Making Our Function Robust

   • Common edge cases (empty strings, non-digits, etc.)

   • Enhanced C implementation with edge case handling

10. Binary, Octal, and Hexadecimal: Beyond Base-10

    • Adapting the algorithm for different bases

    • C implementation for multiple bases

11. Performance Considerations: Optimizing String-to-Number Conversion

    • Optimization techniques

    • Optimized C implementation for chunk processing

12. Memory and Type Considerations: Integers vs. Floating Point

    • Floating-point conversion challenges

    • Simplified floating-point conversion implementation

13. Unicode and Internationalization: Beyond ASCII

    • Unicode digit handling

    • Unicode-compatible conversion implementation

14. The Reverse Process: Converting Numbers to Strings

    • Algorithm for number-to-string conversion

    • C implementation for integer-to-string conversion

15. Real-World Applications and Pitfalls

    • Input validation

    • Custom parsers

    • Common errors to avoid

    • Cross-language consistency

16. Testing and Edge Cases: Ensuring Correctness

    • Testing checklist for robust conversion

    • C test harness implementation

17. Conclusion: The Devil in the Details

    • Summary of key insights

    • Call to share experiences

Introduction: The Hidden Magic Behind parseInt()

Most of us take these conversion functions for granted. We call them daily without a second thought, trusting the black box to do its job. But understanding what's happening internally isn't just academic – it can save you from subtle bugs and help you write more efficient code.

Ever wondered what happens when you convert a string like "123" into a number that a computer can actually do math with? At first glance, it seems simple—after all, we humans can look at the characters "123" and instantly recognize the number 123.

But for computers, which can only process binary data, transforming text into computable numbers requires some fascinating translation work under the hood.

The Core Challenge: Computers Only Understand Numbers

Let's start with a fundamental truth that we often forget: computers can only process and store ones and zeros. They only understand numbers. Everything else – characters, colors, images – must be encoded as numbers for the computer to work with them.

This creates an interesting paradox when we work with numeric input. When a user types "42" into a form field, the computer doesn't receive the number 42. Instead, it receives a sequence of character codes representing the digits '4' and '2'. It's our job as developers to transform these character codes into an actual number that the computer can perform calculations with.

ASCII and Character Encoding: The Missing Link

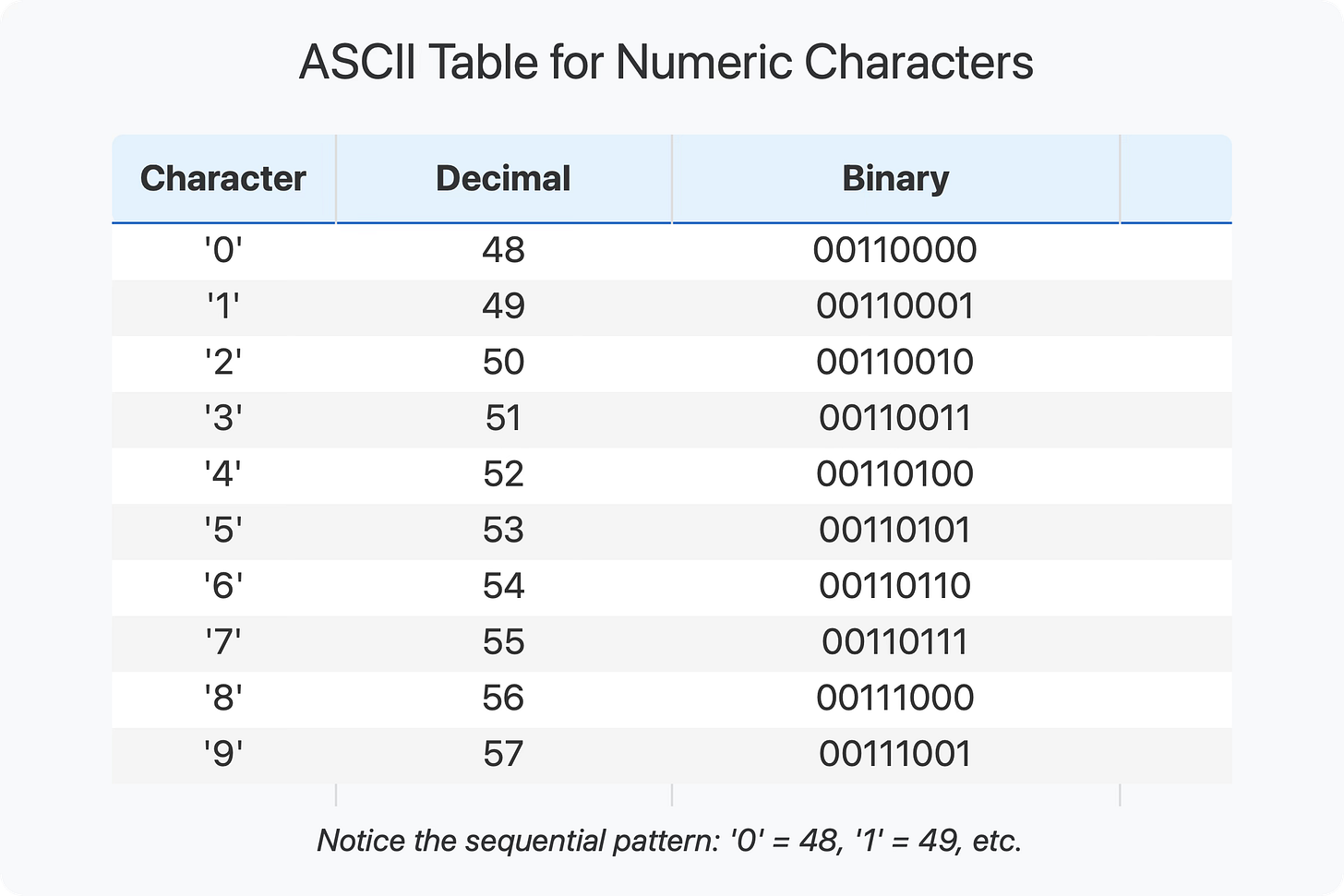
To understand string-to-number conversion, we need to first understand how characters are stored in memory. The most basic encoding system is ASCII (American Standard Code for Information Interchange). In ASCII, each character is associated with a specific binary number.

For example, in ASCII:

• The character '0' is represented by 00110000 (48 in decimal)

• The character '1' is represented by 00110001 (49 in decimal)

• The character '2' is represented by 00110010 (50 in decimal)

And so on up to '9' which is 00111001 (57 in decimal).

Notice something interesting? The numeric characters are grouped together and ordered sequentially. This isn't an accident – it's a deliberate design choice that makes conversion much simpler.

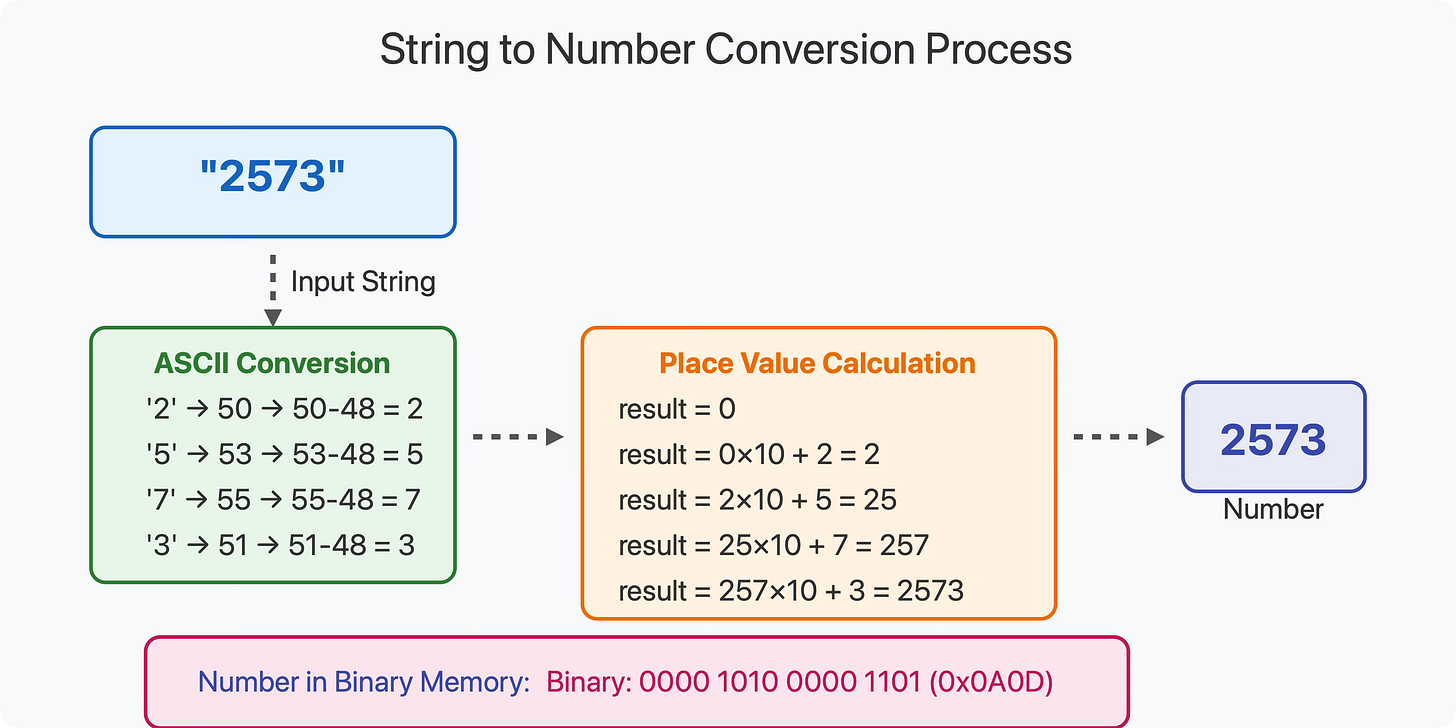
Because of this design, we can convert any numeric character to its actual value by simply subtracting 48 (or '0' in character form) from its ASCII code:

• '0' (ASCII 48) - 48 = 0

• '1' (ASCII 49) - 48 = 1

• '2' (ASCII 50) - 48 = 2

This simple pattern holds true for all numeric digits in ASCII, and it's the foundation of string-to-number conversion.

Why We Can't Just Add ASCII Codes

At this point, you might wonder: if the computer already has the digits stored as numbers (their ASCII codes), why not just use those directly? Let's see why that doesn't work.

Imagine we have the string "53". The ASCII codes for these characters are 53 for '5' and 51 for '3'. If we just added these numbers together, we'd get 104, which is clearly not 53.

This highlights an important distinction: the ASCII code for a digit is not the same as the value that digit represents. We need a proper conversion algorithm.

Multi-Digit Numbers: Position Matters

Converting a single digit is easy – subtract 48 and you're done. But what about multi-digit numbers?

When we write a decimal number like "4327", what we're actually expressing is:

• 7 × 10^0 (units)

• 2 × 10^1 (tens)

• 3 × 10^2 (hundreds)

• 4 × 10^3 (thousands)

When we add these together: (4 × 1000) + (3 × 100) + (2 × 10) + (7 × 1) = 4327

This is the positional number system we use every day. Each digit's position determines its contribution to the final value. Our string-to-number algorithm needs to account for this.

The Algorithm: Building Numbers Digit by Digit

Now that we understand the challenge, let's explore the elegantly simple algorithm that almost every programming language uses to convert strings to numbers.

String to Number Conversion Process

Here's the general approach:

1. Initialize a result variable to 0

2. For each character in the string (from left to right): a. Convert the character to its numeric value (by subtracting '0') b. Multiply the current result by 10 c. Add the numeric value to the result

3. Return the result

Let's trace through this with our example "4327":

1. Start with result = 0

2. Process '4':

   • Convert '4' to 4

   • Multiply result by 10: 0 × 10 = 0

   • Add the value: 0 + 4 = 4

3. Process '3':

   • Convert '3' to 3

   • Multiply result by 10: 4 × 10 = 40

   • Add the value: 40 + 3 = 43

4. Process '2':

   • Convert '2' to 2

   • Multiply result by 10: 43 × 10 = 430

   • Add the value: 430 + 2 = 432

5. Process '7':

   • Convert '7' to 7

   • Multiply result by 10: 432 × 10 = 4320

   • Add the value: 4320 + 7 = 4327

6. Return 4327

This algorithm is beautifully simple, yet it perfectly captures the positional nature of our number system. Each time we multiply by 10, we're essentially shifting all existing digits one place to the left, making room for the new digit.

Implementing the Algorithm in C

Let's see how this algorithm looks in actual code. Here's a simple C implementation:

int string_to_int(const char* str) {
    int result = 0;
    
    while (*str != '\0') {
        // Check if the character is a digit
        if (*str >= '0' && *str <= '9') {
            // Convert char to int and add to result
            result = result * 10 + (*str - '0');
        } else {
            // Handle error: non-digit character
            return -1;
        }
        str++;
    }
    
    return result;
}

This function iterates through each character of the string. For each character, it:

1. Checks if it's a valid digit

2. Multiplies the current result by 10 to shift digits left

3. Adds the numeric value of the current digit

4. Moves to the next character

Note how we use *str - '0' instead of *str - 48. This is more readable and portable, as it doesn't assume a specific character encoding.

Seeing the Algorithm in Action: A JavaScript Implementation

Let's implement this algorithm in JavaScript to see it in action:

function myParseInt(str) {
    let result = 0;
    
    for (let i = 0; i < str.length; i++) {
        // Check if character is a digit
        if (str[i] >= '0' && str[i] <= '9') {
            // Convert char to its numeric value
            const digitValue = str.charCodeAt(i) - '0'.charCodeAt(0);
            
            // Update result: shift left and add new digit
            result = result * 10 + digitValue;
        } else {
            // Non-digit found, stop parsing
            break;
        }
    }
    
    return result;
}

// Test it
console.log(myParseInt("425")); // Outputs: 425

This simple function implements the core algorithm. For each digit character, we:

1. Convert it to its numeric value using the character code difference

2. Multiply our running total by 10 to shift everything left

3. Add the new digit's value

Notice how we didn't need to know the string's length in advance. The algorithm naturally builds the number as it goes.

Handling Edge Cases: Making Our Function Robust

In real-world applications, we need to handle various edge cases:

1. Empty strings: Should return 0 or an error

2. Non-digit characters: Should either ignore them, stop parsing, or return an error

3. Leading/trailing whitespace: Should be trimmed or ignored

4. Positive/negative signs: Should change the sign of the result

5. Overflow/underflow: Should handle numbers outside the valid range

Let's enhance our C implementation to handle some of these:

int string_to_int(const char* str) {
    int result = 0;
    int sign = 1;
    
    // Skip leading whitespace
    while (*str == ' ' || *str == '\t') {
        str++;
    }
    
    // Handle sign
    if (*str == '-') {
        sign = -1;
        str++;
    } else if (*str == '+') {
        str++;
    }
    
    // Process digits
    while (*str != '\0') {
        if (*str >= '0' && *str <= '9') {
            // Check for overflow
            if (result > (INT_MAX - (*str - '0')) / 10) {
                return sign == 1 ? INT_MAX : INT_MIN;
            }
            result = result * 10 + (*str - '0');
        } else {
            // Non-digit character found, stop parsing
            break;
        }
        str++;
    }
    
    return result * sign;
}

This enhanced version handles whitespace, signs, and stops parsing when it encounters invalid characters. It also checks for overflow, though the overflow check is simplified for readability.

Binary, Octal, and Hexadecimal: Beyond Base-10

So far, we've focused on converting decimal (base-10) strings to numbers. But what about other bases like binary (base-2), octal (base-8), or hexadecimal (base-16)?

The good news is that the core algorithm remains the same, with two key differences:

1. The character set changes (for hex, we need to handle 'A' through 'F')

2. Instead of multiplying by 10 each time, we multiply by the appropriate base

Here's a C function that can handle multiple bases:

int string_to_int_base(const char* str, int base) {
    int result = 0;
    
    while (*str != '\0') {
        int digit_value;
        
        if (*str >= '0' && *str <= '9') {
            digit_value = *str - '0';
        } else if (*str >= 'A' && *str <= 'F') {
            digit_value = 10 + (*str - 'A');
        } else if (*str >= 'a' && *str <= 'f') {
            digit_value = 10 + (*str - 'a');
        } else {
            // Invalid character for this base
            return -1;
        }
        
        // Check if digit is valid for this base
        if (digit_value >= base) {
            return -1;
        }
        
        // Update result
        result = result * base + digit_value;
        str++;
    }
    
    return result;
}

This function can handle bases from 2 to 16. For example:

• string_to_int_base("1010", 2) converts the binary string "1010" to 10

• string_to_int_base("FF", 16) converts the hexadecimal string "FF" to 255

Performance Considerations: Optimizing String-to-Number Conversion

While our algorithm is simple and efficient, there are ways to optimize it further:

1. Avoid redundant checks: If we know all characters are valid digits, we can skip validation

2. Use lookup tables: For hexadecimal conversion, a lookup table can be faster than branch conditions

3. Process multiple digits at once: On modern processors, we can process multiple digits in parallel

4. Leverage hardware instructions: Some CPUs have specific instructions for binary-coded decimal operations

Here's a simple optimization that processes digits in chunks:

int optimized_string_to_int(const char* str) {
    int result = 0;
    
    // Process 4 digits at a time
    while (str[0] && str[1] && str[2] && str[3]) {
        if (str[0] < '0' || str[0] > '9' || 
            str[1] < '0' || str[1] > '9' ||
            str[2] < '0' || str[2] > '9' ||
            str[3] < '0' || str[3] > '9') {
            break;
        }
        
        result = result * 10000 + 
                (str[0] - '0') * 1000 +
                (str[1] - '0') * 100 +
                (str[2] - '0') * 10 +
                (str[3] - '0');
        
        str += 4;
    }
    
    // Process remaining digits one by one
    while (*str >= '0' && *str <= '9') {
        result = result * 10 + (*str - '0');
        str++;
    }
    
    return result;
}

This optimization processes digits in groups of 4 when possible, reducing the number of loop iterations. However, it's more complex and may not be worth it for short strings.

Memory and Type Considerations: Integers vs. Floating Point

Our discussion so far has focused on integer conversion, but real-world applications often need to handle floating-point numbers as well. Converting strings like "3.14159" to float or double values follows similar principles but has additional complexities:

1. Detecting and handling the decimal point

2. Supporting scientific notation (e.g., "1.23e-4")

3. Ensuring floating-point precision

Here's a simplified implementation for floating-point conversion:

double string_to_double(const char* str) {
    double result = 0.0;
    int sign = 1;
    double fraction = 0.0;
    double fraction_factor = 0.1;
    bool decimal_seen = false;
    
    // Handle sign
    if (*str == '-') {
        sign = -1;
        str++;
    } else if (*str == '+') {
        str++;
    }
    
    // Process digits
    while (*str != '\0') {
        if (*str >= '0' && *str <= '9') {
            if (!decimal_seen) {
                result = result * 10.0 + (*str - '0');
            } else {
                fraction += (*str - '0') * fraction_factor;
                fraction_factor *= 0.1;
            }
        } else if (*str == '.' && !decimal_seen) {
            decimal_seen = true;
        } else {
            // Invalid character or second decimal point
            break;
        }
        str++;
    }
    
    return sign * (result + fraction);
}

This function handles basic floating-point conversion but doesn't support scientific notation or check for overflow. A production-ready version would need these features and careful handling of floating-point precision issues.

Unicode and Internationalization: Beyond ASCII

Our examples have assumed ASCII encoding, but modern applications often use Unicode, which supports characters from virtually all writing systems. The good news is that digits in most scripts follow similar patterns to ASCII digits

ASCII Table for Numeric Characters

In Unicode:

• ASCII digits '0' to '9' have code points U+0030 to U+0039

• Arabic-Indic digits '٠' to '٩' have code points U+0660 to U+0669

• Devanagari digits '०' to '९' have code points U+0966 to U+096F

Each set follows the same pattern: consecutive code points for consecutive digits. This means our conversion algorithm can work with minimal modifications:

int unicode_string_to_int(const wchar_t* str) {
    int result = 0;
    
    while (*str != L'\0') {
        if (*str >= L'0' && *str <= L'9') {
            // ASCII digits
            result = result * 10 + (*str - L'0');
        } else if (*str >= L'٠' && *str <= L'٩') {
            // Arabic-Indic digits
            result = result * 10 + (*str - L'٠');
        } else if (*str >= L'०' && *str <= L'९') {
            // Devanagari digits
            result = result * 10 + (*str - L'०');
        } else {
            // Not a recognized digit
            return -1;
        }
        str++;
    }
    
    return result;
}

This function can convert strings containing digits from different scripts. In practice, you'd want to use standard libraries that handle Unicode properly and account for all possible digit forms.

The Reverse Process: Converting Numbers to Strings

As mentioned in the reference, there's also a reverse process: converting numbers back into strings. This is what happens when you call functions like printf() or toString().

The algorithm for this is essentially the reverse of what we've discussed:

1. Repeatedly divide the number by 10, collecting the remainders

2. Convert each remainder to its corresponding character by adding the code for '0'

3. Reverse the resulting string (since we process digits from least to most significant)

Here's a simple implementation:

void int_to_string(int num, char* str) {
    int i = 0;
    bool is_negative = false;
    
    // Handle 0 explicitly
    if (num == 0) {
        str[i++] = '0';
        str[i] = '\0';
        return;
    }
    
    // Handle negative numbers
    if (num < 0) {
        is_negative = true;
        num = -num;
    }
    
    // Process digits
    while (num != 0) {
        int remainder = num % 10;
        str[i++] = remainder + '0';
        num = num / 10;
    }
    
    // Add negative sign if needed
    if (is_negative) {
        str[i++] = '-';
    }
    
    // Null-terminate the string
    str[i] = '\0';
    
    // Reverse the string
    int start = 0;
    int end = i - 1;
    while (start < end) {
        char temp = str[start];
        str[start] = str[end];
        str[end] = temp;
        start++;
        end--;
    }
}

This function converts an integer to a string, handling negative numbers and zero properly. It's a good exercise to extend it to handle other bases and floating-point numbers.

Real-World Applications and Pitfalls

Understanding string-to-number conversion is not just academic – it has practical applications and can help you avoid common pitfalls:

1. Input Validation

When validating user input, knowing how conversion works helps you catch and handle errors properly. For example, you might want to distinguish between:

• Completely invalid input ("abc")

• Partially valid input ("123abc")

• Valid input with leading/trailing spaces (" 123 ")

2. Custom Parsers

While standard libraries provide parsing functions, you sometimes need custom parsers for:

• Domain-specific number formats (e.g., currency with thousands separators)

• Non-standard bases (e.g., base-36)

• Performance-critical code paths

3. Avoiding Common Errors

Understanding the conversion process helps avoid common errors:

• Integer overflow during conversion

• Loss of precision when parsing floating-point values

• Incorrect handling of negative numbers

• Locale-specific issues (e.g., decimal points vs. commas)

4. Cross-Language Consistency

Different languages handle string-to-number conversion slightly differently. Understanding the underlying algorithm helps ensure consistent behavior across languages.

Testing and Edge Cases: Ensuring Correctness

A robust string-to-number conversion function should handle various edge cases correctly. Here's a testing checklist:

• Empty strings

• Strings with only whitespace

• Positive and negative numbers

• Leading/trailing zeros

• Minimum and maximum values for the target type

• Values that cause overflow

• Invalid characters in different positions

• Different locales and encodings

• Performance with very long strings

Here's a simple test harness for our C implementation:

void test_string_to_int() {
    struct TestCase {
        const char* input;
        int expected;
        bool should_fail;
    };
    
    struct TestCase test_cases[] = {
        {"0", 0, false},
        {"1", 1, false},
        {"-1", -1, false},
        {"123", 123, false},
        {"-456", -456, false},
        {"2147483647", INT_MAX, false},  // Max int
        {"-2147483648", INT_MIN, false},  // Min int
        {"", 0, true},                    // Empty string
        {"abc", 0, true},                 // Invalid characters
        {"12a34", 0, true},               // Invalid in the middle
        {"2147483648", 0, true},          // Overflow
    };
    
    int num_tests = sizeof(test_cases) / sizeof(test_cases[0]);
    int passed = 0;
    
    for (int i = 0; i < num_tests; i++) {
        int result;
        bool failed = false;
        
        // Try to convert, catch errors
        result = string_to_int(test_cases[i].input);
        failed = (result == -1);  // Assuming -1 means error
        
        if (failed == test_cases[i].should_fail) {
            if (!failed && result == test_cases[i].expected) {
                passed++;
                printf("Test %d passed: \"%s\" -> %d\n", 
                       i, test_cases[i].input, result);
            } else if (failed) {
                passed++;
                printf("Test %d passed: \"%s\" -> (error as expected)\n", 
                       i, test_cases[i].input);
            } else {
                printf("Test %d failed: \"%s\" -> %d (expected %d)\n", 
                       i, test_cases[i].input, result, test_cases[i].expected);
            }
        } else {
            printf("Test %d failed: \"%s\" -> %s (unexpected)\n", 
                   i, test_cases[i].input, failed ? "error" : "success");
        }
    }
    
    printf("%d/%d tests passed\n", passed, num_tests);
}

This test harness checks various inputs against expected outputs, helping ensure our function handles edge cases correctly.

Conclusion: The Devil in the Details

String-to-number conversion is a fundamental operation that seems simple on the surface but has surprising depth. Understanding how it works under the hood gives you better control over your code and helps you write more robust applications.

The next time you call parseInt(), atoi(), or any similar function, remember the elegant algorithm working behind the scenes, converting characters to digits, shifting positions, and building up the result one digit at a time.

In programming, as in life, the devil is in the details. Taking the time to understand these foundational algorithms makes you a better developer and gives you a deeper appreciation for the tools we use every day.

Now, I'd love to hear from you. Have you ever encountered strange behavior with string-to-number conversion? Or perhaps you've implemented custom parsers for specific use cases? Share your experiences in the comments!