Why Processor Bit Counts Are Powers of 2?

A Deep Dive into Architecture, History, and Efficiency of Processor Bits

Introduction

From the Intel 8086 to modern 64-bit processors, most CPUs have bit counts that are powers of 2 (8, 16, 32, 64). This design choice isn’t arbitrary—it’s rooted in binary logic, hardware efficiency, and historical evolution.

In this article, we’ll explore why powers of 2 dominate processor architecture, examine exceptions and demonstrate how software and hardware leverage these designs.

---

Table of Contents

1. The Binary Foundation

2. Historical Context: The 8-Bit Byte Revolution

3. Memory Alignment and Access Efficiency

4. Address Bus and Memory Mapping

5. Hardware Simplification: Counters and Registers

6. Exceptions to the Rule

7. Code Examples: Efficiency in Practice

8. Modern Architectures: 64-Bit and Beyond

9. Conclusion

1. The Binary Foundation

Computers operate in binary (base-2), where each bit is a 0 or 1. Powers of 2 align naturally with this system, simplifying operations like addressing, arithmetic, and data alignment.

Key Concepts:

• Bit: The smallest unit of data (0 or 1).

• Byte: 8 bits (adopted as standard in the 1960s).

• Word Size: Number of bits a CPU processes at once (e.g., 32-bit, 64-bit).

Example: A 32-bit register can hold values from 0 to 232−1232−1.

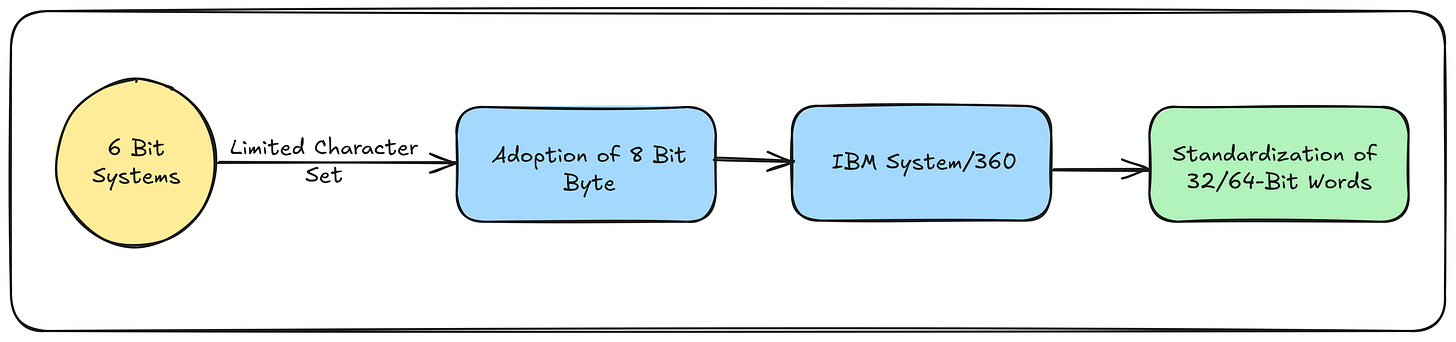
2. Historical Context: The 8-Bit Byte Revolution

The IBM System/360 (1964) popularized the 8-bit byte, balancing character encoding (ASCII) and numeric efficiency (two BCD digits per byte).

Why 8 Bits?

• Character Encoding: 8 bits allowed 256 characters (vs. 64 with 6 bits).

• Numeric Storage: Two Binary-Coded Decimal (BCD) digits fit in one byte.

• Hardware Compatibility: Aligned with emerging memory and bus designs.

3. Memory Alignment and Access Efficiency

Processors fetch data in fixed-size blocks. Aligning data to power-of-two boundaries reduces memory access and hardware complexity.

Example: 32-bit Data Access

• Aligned Address (0x0000): Single fetch.

• Unaligned Address (0x0001): Requires two fetches and shifting.

Code Snippet (C):

#include <stdio.h>
#include <stdint.h>
#include <inttypes.h>

struct AlignedStruct {
    uint32_t a; // 4 bytes, aligned to 4
    uint32_t b; // 4 bytes, aligned to 8
} __attribute__((aligned(8)));

struct UnalignedStruct {
    uint32_t a;
    uint32_t b;
} __attribute__((packed));

int main() {
    printf("Aligned size: %zu\n", sizeof(struct AlignedStruct));  // Output: 8
    printf("Unaligned size: %zu\n", sizeof(struct UnalignedStruct)); // Output: 8 (but may require extra cycles)
    return 0;
}

---

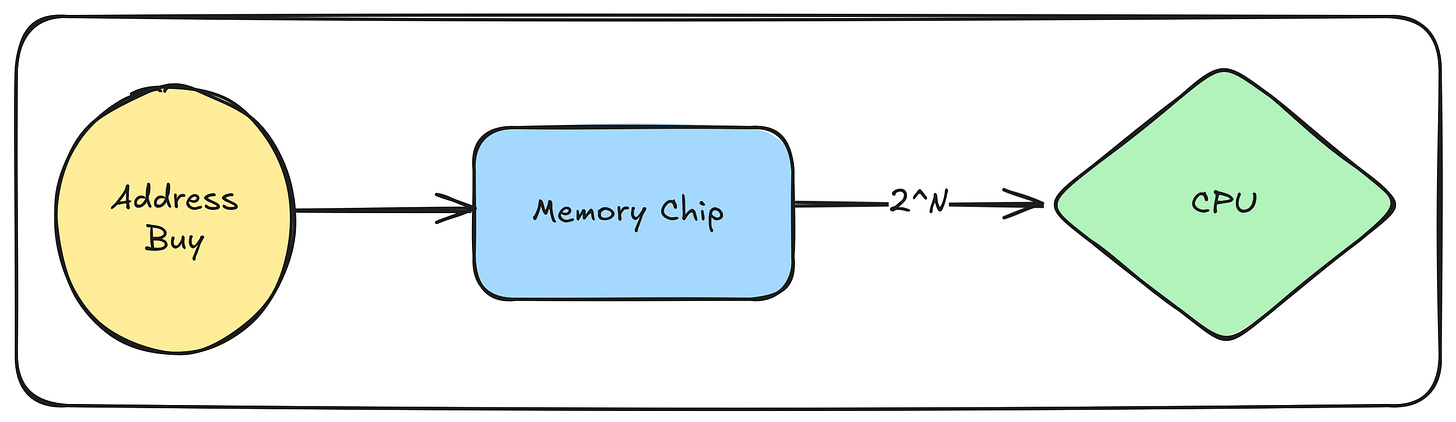
4. Address Bus and Memory Mapping

An NN-bit address bus can access 2^N locations. Powers of 2 maximize addressable space without fragmentation.

Example:

• 16-bit address bus → 65,536 addresses.

• 20-bit (Intel 8086) → 1,048,576 addresses via segmentation.

5. Hardware Simplification: Counters and Registers

Power-of-2 sizes simplify counters and logic circuits.

3-Bit Counter Example:

• Counts 0–7 (8 states) for 8-bit bytes.

• Non-power-of-2 (e.g., 12 bits) requires 4-bit counters with unused states.

Verilog Code:

module Counter3Bit (input clk, output reg [2:0] count);  
always @(posedge clk)  
    count <= count + 1; // Cycles through 0-7  
endmodule  

6. Exceptions to the Rule

6.1 Intel 8086 (20-bit Address Bus)

Used segmentation to access 1 MB of memory:

• Segment register (16-bit) << 4 + Offset (16-bit) = 20-bit address.

6.2 24-Bit Systems (ICL 1900)

• 6-bit bytes, limited to uppercase text.

• Phased out due to inefficiency.

7. Code Examples: Efficiency in Practice

7.1 Bitmasking vs. Division

# Power-of-2 modulus using bitmasking (fast)  
def mod_power_of_two(num, divisor):  
    return num & (divisor - 1)  

print(mod_power_of_two(15, 8))

7.2 Hash Tables with Power-of-2 Sizes

#define TABLE_SIZE 1024 // 2^10  

unsigned int hash(int key) {  
    return key % TABLE_SIZE;  
    // Equivalent to: key & (TABLE_SIZE - 1)  
}  

8. Modern Architectures: 64-Bit and Beyond

8.1 Why 64-Bit?

• Addresses 264264 bytes (16 exabytes).

• Future-proofing and compatibility.

8.2 RISC-V and 128-Bit Possibilities

• RISC-V ISA supports 128-bit extensions.

• Current implementations use 64-bit, reserving bits for future use.

9. Conclusion

Power-of-2 bit counts simplify hardware design, memory access, and software optimization. While exceptions exist, the benefits of binary alignment ensure this trend continues. As computing evolves, 64-bit architectures will dominate until new paradigms emerge.

Further Reading

• IBM System/360 Technical Journal (1964).

• Intel® 64 and IA-32 Architectures Software Developer Manuals.

• RISC-V ISA Specification.

This exploration highlights the intersection of history, engineering, and mathematics that shapes modern computing. Whether writing low-level code or designing hardware, understanding these principles is key to building efficient systems.